Advent Of Code 2021 Days 16-20
o
Advent of Code 2021 Days 16-20

Welcome back to some more Advent of Code 2021!
These posts will be quite brief, just a few thoughts on each puzzle and the Python 3 code I used to solve it. All code on Github here. The code below is for Part 2 of each day, which often incorporates Part 1 in some way.
Day 16 - Packet Decoder
Thoughts
A parsing puzzle - formerly my least favourite type of AoC puzzle, though they are growing on me. A little. Here our puzzle input is a transmission in hexadecimal. The transmission consists of a single packet, which itself contains multiple packets.
Packet Structure
When converted into binary, a packet is structured as follows:
- The first 3 bits encode an integer which is the packet version
- The next 3 bits encode another integer, which is the type ID.
- If ID == 4, the packet is a literal value, representing a single binary integer
- Otherwise, the packet is an operator packet, and the ID determines which operation it performs on all the subpackets it contains (see below)
All packets will have this standard 6-digit header.
Literal Value Packets
Literal values have their header followed by groups of five bits. The first bit in each 5-bit group is 1, unless it is the last group contained in the packet, in which case it is 0. The last 4 digits in each group are the digits the binary number the packet represents, padded with leading zeros and split into groups of exactly four digits.
For example, a literal value packet, converted from hexadecimal to binary, might look like this: 111100100101011010001. The interpretation of this packet is explained by the diagram below:
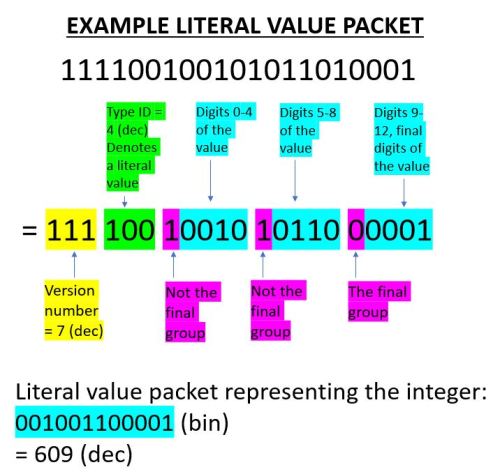
Operator Packets
If the type ID of an operator packet isn’t equal to 4, the packet is an operator packet. The type ID defines the operation that the packet performs on the subpackets it contains.
| Type ID | Packet value |
|---|---|
| 0 | Sum of the values of the subpackets |
| 1 | Product of the values of the subpackets |
| 2 | Minimum value of the subpackets |
| 3 | Maximum value of the subpackets |
| 5 | 1 if the first subpacket’s value is greater than the second. 0 otherwise. Will contain exactly two subpackets. |
| 6 | 1 if the first subpacket’s value is less than the second. 0 otherwise. Will contain exactly two subpackets. |
| 7 | 1 if the first subpacket’s value is equal to the second. 0 otherwise. Will contain exactly two subpackets. |
After the 6-digit header containing version number and type ID, the next digit in an operator packet is the length type. This determines how to work out which subpackets are included.
If length type is 0, then the next 15 bits of the packet represent an integer which is the total length in bits of the of the subpackets contained by the operator packet.
If length type is 1, then the next 11 bits of the packet represent an integer which is the number of subpackets contained by the operator packet. This only counts the “immediate” subpackets, i.e. nested subpackets to do not count towards this total.
Below is an example of an operator subpacket using length type 1, with value 4 + 3 = 7.
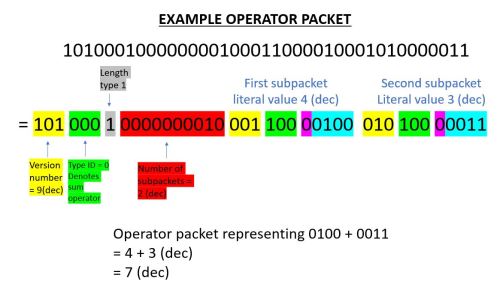
And another example using length type 0, with value 4 x 3 = 12.

Approach
I used a little bit of object-oriented programming here, which I normally don’t see as beneficial for Advent of Code puzzles. Here we need to keep track of where we are in a binary string as we parse it, and the easiest thing seemed to be to have a Message object where the string and the current position are attributes.
The Message class has a helper method integer_value to pull out a decimal integer value for the next few digits in the binary string, the number of digits specified as an argument.
It also has two methods parse_one_packet and read_packet_content, which together constitute a parser. Given a packet (which may or may not contain subpackets), parse_one_packet will convert the packet into a tuple containing the version number, the type ID, and the content of the packet. The content is either an integer (for literal value packets) or a list of tuples representing each of the subpackets (for an operator packet).
Evaluating a packet’s value is left to an external function apply_operators, outside the Message class, which takes in the parsed (tuple) version of a packet and applies the operations required by the puzzle rules.
Python Code
import sys
import binascii
import math
class Message:
def __init__(self, file):
hex_data = file.read().strip()
#convert transmission from hexadecimal to binary
bin_data = binascii.a2b_hex(hex_data)
#pos is an integer attribute representing the current position of the parser in parsing the message
self.pos = 0
#bits is a string attribute containing the bits in the message
self.bits = ''
#add the bits from the input file into the bits attribute of the Message object
for byte in bin_data:
self.bits += '{:08b}'.format(byte)
def integer_value(self, n_bits):
#returns the integer value, in decimal, of the next n_bits bits of the message
#convert to decimal and store as int
result = int(self.bits[self.pos:self.pos+n_bits], 2)
#advance the position
self.pos += n_bits
return result
def parse_one_packet(self):
#parse the next packet of the message
#return the packet as a tuple of (packet version, type id, packet content)
#content is either a decimal integer (for literal value packets), or a list of subpackets (for operator packets)
version = self.integer_value(3)
id = self.integer_value(3)
content = self.read_packet_content(id)
return (version, id, content)
def read_packet_content(self,id):
#interpret the contents of a packet
if id == 4: #the packet is a literal value, return the decimal integer value
val = ''
go = 1
while go == 1:
go = self.integer_value(1)
val += "{:04b}".format(self.integer_value(4))
return int(val,2)
else: #the packet is an operator packet, return a list of subpackets
length_type = self.integer_value(1)
if length_type == 1: #the next 11 binary digits give the number of subpackets
n_packets = self.integer_value(11)
return [self.parse_one_packet() for _ in range(n_packets)]
if length_type == 0: #the next 15 binary digits give the total number of bits in the subpackets
x = self.integer_value(15) #need to do this on a separate line as it changes self.pos
end = self.pos + x #end = self.pos + self.integer_value(15) one one line would be bad as it would depend on the order that pos and integer_value are evaluated
output=[]
while self.pos < end: #parse packets until the end position is reached
output.append(self.parse_one_packet())
return output
def apply_operators(packet):
#recursive function to calculate the value of a packet (which may contain more packets, which may contain more packets etc.)
(version, id, content) = packet
if id==0: #sum packet, calculates the sum of all subpackets
total = 0
for subpacket in content:
total += apply_operators(subpacket)
return total
if id==1: #product packet, calculates the product of all subpackets
total = 1
for subpacket in content:
total = total * apply_operators(subpacket)
return total
if id == 2: #minimum packet, calculates the minimum value of all subpackets
total = math.inf
for subpacket in content:
val = apply_operators(subpacket)
if val<total:
total = val
return total
if id == 3: #maximum packet, calculates the maximum value of all subpackets
total = -math.inf
for subpacket in content:
val = apply_operators(subpacket)
if val>total:
total = val
return total
if id==4: #literal value packet, the value in content is the integer the packet represents
total = content
return total
if id==5: # > packet. contains exactly two subpackets, if the first has a value greater than the second, return 1. Otherwise return 0.
total = 0
if apply_operators(content[0]) > apply_operators(content[1]):
total = 1
return total
if id==6: # < packet. contains exactly two subpackets, if the first has a value less than the second, return 1. Otherwise return 0.
total = 0
if apply_operators(content[0]) < apply_operators(content[1]):
total = 1
return total
if id==7: # == packet. contains exactly two subpackets, if the first has a value equal to the second, return 1. Otherwise return 0.
total = 0
if apply_operators(content[0]) == apply_operators(content[1]):
total = 1
return total
#initialise a Message object from the input file
with open(sys.argv[1]) as file:
message = Message(file)
#parse the outer packet of the message into a tuple of (version number, type ID, content)
packet = message.parse_one_packet()
#calculate the value of the outer packet of the message
print(apply_operators(packet))
Day 17 - Trick Shot
Thoughts
What we have here is a simplified version of projectile motion with gravity and water resistance on a 2-dimensional grid. We are launching an underwater probe from the origin and then computing its position after each step. The probe starts at position (0,0) with initial velocity (ux,uy), where ux and uy are integers.
On each step:
- The probe’s x-position increases by its current x-velocity.
- Then the probe’s y-position increases by its current y-velocity.
- Then the probe’s x-velocity decreases by 1 if it is positive, increases by 1 if it is negative, or stays unchanged if it is zero. This simulates the water resistance or drag on the probe.
- Then the probe’s y-velocity decreases by 1, simulating gravity.
The goal is to find all the distinct values of the initial velocity vector which result in the probe being in a specified target area after any step. The target area is a rectangle specified by integer minimum and maximum coordinates x_min, x_max, y_min and y_max.
For the example and my input, x_max>0, y_min<0 and y_max<0, which I have assumed in my solution below.
This problem can be solved analytically, but it can also be brute forced pretty quickly. Unsurprisingly, I chose the latter. The solution below simulates a range of initial velocities and computes whether the probe hits the target area for each case, incrementing a count if the probe does reach the target area after any step.
Bounds on the initial x-velocity
The code tries integer values for ux between 1 and x_max inclusive.
- If
ux <= 0, the x-velocity will be always be negative or zero. This means the probe will never move right of the origin, and sincex_min>0, the target area is always right of the origin. - If
ux > x_max, then the probe overshoots to the right of the target area on the first step. Since x-velocity was initially positive and tends towards zero, this overshoot can never be corrected.
Bounds on the initial y-velocity
The code tries integer values for uy between y_min and -y_min-1 inclusive. (Recall that I have assumed y_min<0).
- If
uy < y_minthen the probe falls below the target area after the first step. Since y-velocity can only decrease, this means the probe will always be below the target area after every step. - I’ve assumed that
y_max<0. For any positiveuy, the probe starts at(0,0)and passes throughy=0again with velocity-uy-1.- If
-uy-1 < y_min, or equivalentlyuy > -y_min-1, then the probe will fall below the target area after the following step.
- If
Python Code
import sys
#read the input data to find the boundaries of the target area
with open(sys.argv[1]) as file:
data = file.read().strip()
data = data.replace('target area: x=','').replace('y=','').replace('..',', ').split(', ')
x_min = int(data[0])
x_max = int(data[1])
y_min = int(data[2])
y_max = int(data[3])
def on_target(vx, vy):
#determine whether an initial velocity (vx,vy) results in the probe
#being inside the target area after any step
x=0
y=0
while y>=y_min: #while the probe is above the bottom of the target area
#once it goes below the target area it will never be on target
#as y-velocity is always decreasing
x += vx
y += vy
if x_min <= x <= x_max and y_min <= y <= y_max: #if the position is in the target area
return True
if vx > 0:
vx -= 1
if vx == 0:
if x<x_min or x>x_max:
return False #if the probe is left or right of the target area and has x-velocity zero
#it will never reach the target area
if vx < 0:
vx += 1
vy -= 1
return False
on_target_probes = 0
for ux in range(1,x_max+1):
for uy in range(y_min,-y_min):
is_on_target = on_target(ux,uy)
if is_on_target == True:
on_target_probes += 1
print(on_target_probes)
Day 18 - Snailfish
Thoughts
Snailfish, as is to be expected, have their own version of arithmetic.
- A snailfish number is a pair, such as
[3,4].- The elements of the pair might be an integer or another pair.
[6,[3,[12,4]]is also a valid snailfish number.- Order matters.
[4,3]is a different number to[3,4].
- Snailfish addition is performed by forming a new pair, so that
[3,4] + [7,2] = [[3,4],[7,2]]- Snailfish addition is not commutative:
A + Bis not necessarily equal toB + A.
- Snailfish addition is not commutative:
- Snailfish numbers must be reduced whenever possible. To reduce a snailfish number, apply the first action in the list below that is possible. Once that has been applied, return to the top of the list and apply the first possible action from this list again. Repeat until neither action is possible.
- The leftmost pair that is nested inside 4 pairs explodes
- The leftmost integer that is 10 or greater splits
- To add a list of snailfish numbers, add the first and second, reduce the result, and add the reduced result to the third snailfish number in the list. Then reduce the answer, add the fourth snailfish number, reduce the answer, and so on until the list has been exhausted.
Exploding a pair
To explode a pair, follow the steps below. “Add” here refers to normal addition of integers, not snailfish addition of pairs.
- Add the left element of the pair to the first integer to the left of the pair, if any.
- Add the right element of the pair to the first integer to the right of the pair, if any.
- Replace the exploded pair with the integer
0.
[[[[5,**[2,3]**],6],1]] becomes [[[[**5+2**,**0**],**6+3**],1]] = [[[[7,0],9],1]]
Thanks to a well-formed puzzle input, we can reliably assume that no integer will be nested more than 5 brackets deep at any stage, so we do not need a procedure for exploding a pair where one or more of the elements is another pair. All pairs that explode will be pairs of two integers.
Splitting an integer
To split an integer greater than 9, replace it with a pair as follows:
- The left element of the new pair is the original integer divided by 2 and rounded down
- The right element of the new pair is the original integer divided by 2 and rounded up
10 splits to [5,5]
13 splits to [6,7]
etc.
Magnitude
The magnitude operation maps any reduced snailfish number to an integer. It follows the following rules:
- The magnitude of an integer is equal to the integer itself
- The magnitude of a pair is equal to 3 times the magnitude of its left element, plus 2 times the magnitude of its right element
The Puzzle
We are given a list of snailfish numbers. In part 1, we need to add up the entire list, and calculate the magnitude of the final result. In part 2, we need to find the largest magnitude we can make by adding two distinct snailfish numbers from the list.
My Approach
Here I really wanted to deal with snailfish numbers in a flattened form, without all this nesting.
To that end I convert every snailfish number into a list of tuples (x, depth), one for each integer x inside the snailfish number. depth is calculated as follows: the number of [ symbols to the left of x, minus the number of ] symbols to the left of x.
The snailfish number [6,[3,[12,4]] becomes the list [(6,1), (3,2), (12,3), (4,3)]
The snailfish number [[[[5,[2,3]],6],1]] becomes the list [(5,4), (2,5), (3,5), (6,3),(1,2)]
Each of the operations we require can be performed on the flattened representation of the snailfish number.
Snailfish Addition in Flattened Form
Snailfish addition means appending the second list to the first, then increasing all depths in the new list by 1.
[(1,3), (2,3), (3,2), (4,1)] + [(5,1), (6,1)] -> [(1,4), (2,4), (3,3), (4,2),(5,2), (6,2)]
is equivalent to this sum in the original representation:
[[[1,2],3],4] + [5,6] = [[[[1,2],3],4],[5,6]]
Explosion in Flattened Form
Exploding a pair means:
- Identify the leftmost pair two consecutive integers which have a depth of 5. Call the integer values
aand b.- So the list is of the form
[…, (a,5), (b,5), …]
- So the list is of the form
- Add
ato the nearest integer to the left of the pair (if any) - Add
bto the nearest integer to the right of the pair (if any) - Remove the
(b,5)tuple from the list - Replace the
(a,5)tuple with(0,4).
This explosion example from above:
[[[[5,**[2,3]**],6],1]] -> [[[[7,0],9],1]]
Becomes the following in the flattened representation:
[(5,4), **(2,5)**, **(3,5)**, (6,3), (1,2)] -> [(7,4), (0,4), (9,3), (1,2)]
Splitting in Flattened Form
Splitting an integer means:
- Identify the leftmost integer value in the list that is greater than 9
- So the list is of the form [
…, (x,d), …]wherex>9anddis the depth ofx.
- So the list is of the form [
- Insert the tuple
(ceil(x/2),d+1)in the list directly after(x,d) - Replace the tuple
(x,d)with(floor(x/2), d+1)
So (10,d) splits to (5,d+1) and (5,d+1)
and (13,d) splits to (6,d+1) and (7,d+1)
Magnitude in Flattened Form
Finding the magnitude of a snailfish number ends up being the most complicated task in this flattened representation. My solution is as follows:
- Find the pair (or pairs) of integers with the greatest depth.
- The list would be of the form
[…, (L1,d_max), (R1,d_max), …, `(L2,d_max), (R2,d_max)`, `…`]
- The list would be of the form
- Replace each pair at maximum depth as follows:
(L1,d_max), (R1,d_max) -> (3*L1 + 2*R1, d_max - 1)(L2, d_max), (R2, d_max) -> (3*L1 + 2*R2, d_max - 1)- etc.
- Repeat steps 1 and 2 until the list contains only two tuples
(x, d)and(y,d). - Return
3*x + 2*y.
Python Code
from math import ceil, floor
import sys
from functools import reduce
def read(snail_string): #assume no values above 9 in input
snail = []
depth = 0
for char in snail_string:
if char == '[':
depth += 1
elif char == ']':
depth -= 1
elif char != ',':
snail.append((int(char),depth))
return snail
def explode(snail):
newsnail = snail[:]
for i, (val,depth) in enumerate(snail):
if depth==5:
if i-1>=0:
newsnail[i-1] = (snail[i-1][0]+val,snail[i-1][1])
if i+2<=len(snail)-1:
newsnail[i+2] = (snail[i+2][0]+snail[i+1][0],snail[i+2][1])
newsnail.pop(i+1)
newsnail[i] = (0,depth-1)
return newsnail
return False
def split(snail):
newsnail = snail[:]
for i, (val,depth) in enumerate(snail):
if val > 9:
leftval = int(floor(val/2))
rightval = int(ceil(val/2))
newsnail[i] = (leftval,depth+1)
newsnail.insert(i+1, (rightval,depth+1) )
return newsnail
return False
def add(snail1, snail2):
res = snail1 + snail2
res= [(val,depth+1) for (val,depth) in res]
return res
def snail_reduce(snail):
while explode(snail) or split(snail):
ex = explode(snail)
spl = split(snail)
if ex:
snail = ex
elif spl:
snail = spl
return snail
def add_and_snail_reduce(snail1,snail2):
res = add(snail1,snail2)
res = snail_reduce(res)
return res
def magnitude(snail):
if len(snail) == 2:
return 3*snail[0][0] + 2*snail[1][0]
max_depth = max([d for _,d in snail])
i = 0
while i <= len(snail)-2:
if snail[i][1]==max_depth:
snail[i] = (3*snail[i][0] + 2*snail[i+1][0],max_depth-1)
snail.pop(i+1)
i += 1
else:
i +=1
return magnitude(snail)
def part_one(snails):
return magnitude(reduce(add_and_snail_reduce,snails))
def part_two(snails):
mags = []
for i in range(len(snails)):
for j in range(len(snails)):
if i==j:
continue
mag1 = magnitude(add_and_snail_reduce(snails[i],snails[j]))
mag2 = magnitude(add_and_snail_reduce(snails[j],snails[i]))
mags += [mag1,mag2]
return max(mags)
with open(sys.argv[1]) as file:
snails = [read(line.strip()) for line in file]
print(part_one(snails))
print(part_two(snails))
Day 19 - Beacon Scanner
Thoughts
This was without a doubt the trickiest puzzle so far, for me.
The key objects in the puzzle are scanners and beacons, floating at particular integer coordinates in a 3D underwater space. Each scanner reports the relative position (coordinates) of all the beacons within its range. A scanner does not know its own position or orientation relative to other scanners. The scanner could be rotated any multiple of 90 degrees around any of the three axes, leading to 24 possible orientations.
The Rule of 12
The puzzle asserts that if scanner X can be transformed (reoriented and translated) such that it shares at least 12 sets of beacon coordinates with scanner Y, then we have found the true relative position and orientation of scanner X relative to scanner Y and vice-versa.
This assumption rules out the possibility that we might match, say, 13 beacons from two scanners by pure luck, without having actually found the true relative position and orientation. The rule says that if 12 or more beacons coincide, we have definitely found the true position with no possibility of error.
Puzzle Goal
Our goal is to find the position and orientation of all the scanners, and then calculate the largest Manhattan distance between any two scanners.
My Approach
The approach below is my old friend brute force. Taking scanner 0 as the reference set of coordinates, the code creates a “base scanner” containing all the beacon coordinates from scanner 0.
Then the code iterates through the other scanners in the input. For each scanner, let’s call it scanner B, we iterate over all 24 possible orientations of scanner B, and then over all the possible translations (offsets) which cause at least one beacon from scanner B to align with a beacon from the base scanner.
During that iteration, if we find an orientation and offset that causes at least 12 beacons to align, we know we have found the true orientation and position of scanner B in the coordinate system of the base scanner. We add the (properly oriented and offset) beacon coordinates from scanner B into the base scanner, add scanner B to our list of “visited” scanners, and repeat the whole set of iterations. This continues until all the scanners have been “visited”.
The code keeps a list of the positions (offsets) of each new scanner once it has been translated and aligned. At the end all the Manhattan distances between pairs of scanners are calculated, and the maximum selected.
“sigs” and “perms” - How I constructed the orientations
We can only rotate a scanner by multiples of 90 degrees around each of the coordinate axes. We can’t perform any reflections, or rotate it by any angle that isn’t a multiple of 90 degrees. There’s a set of rotation matrices that expresses the 24 possible rotations, but my code doesn’t use rotation matrices.
Instead, I considered what happens to the coordinates of a beacon when the scanner is rotated.
The first thing that might happen, is some of the coordinates might swap sign. For example a scanner pointing “north” might measure a beacon’s x-coordinate as 52. Rotate the same scanner to point “south” and that x-coordinate would now be measured as -52.
These sign swaps are represented by what I call “signatures” or sigs. A sig is a tuple like (-1,1,-1) which describes which coordinates (x,y,z) will have their signs swapped. The sig (-1,1,-1) would map the beacon coordinates (-3, 5, 6) onto (3, 5, -6) and so on.
In addition to sign swaps, some of the coordinates might change position in the coordinate tuple. For example the coordinates (-3,5,6) might appear as (5,6,-3) to a rotated scanner. This is just a permutation of the coordinates. These are expressed as tuples (“perms”) of the indices (0,1,2) with 0 representing the original x-axis, 1 the original y-axis, and 2 the original z-axis. Turning (-3,5,6) to (5,6,-3) is achieved using the perm (1,2,0).
An overabundance of orientations
There are 2^3^ = 8 possible sigs:
{(1,1,1), (-1,1,1), (-1,-1,1), (-1,1,-1), (-1,-1,-1), (1,-1,1), (1,-1,-1), (1,1,-1)}
There are 6 possible permutations of 3 axes, leading to 6 perms:
{(0,1,2), (0,2,1), (1,2,0), (1,0,2), (2,0,1), (2,1,0)}
Every orientation consists of applying a sig and a perm, so there are 8 x 6 = 48 possible orientations…wait a second, something has gone wrong! The problem here is that those 48 orientations include reflections! The scanners are underwater, they might have got turned around somewhat, but they have not been replaced by invaders from the Mirror Universe! Reflections are not valid for this puzzle.
Even/Odd Parity
How do we get rid of the reflections? We need to make sure that the overall parity of the reorientation is even, so that it keeps the coordinate system right-handed. This means we are avoiding any net reflection in our reorientation.
An even sig contains an even number of negative elements.
An even perm has an even number of pairs of indices which are out of ascending order.
e.g. (2,0,1). Consider all 3 pairs of indices:
- (2,0) out of order
- (0,1) in order
- (2,1) out of order.
Two pairs are mis-ordered, so the perm is even.
e.g. (0,2,1).
- (0,2) in order
- (0,1) in order,
- (2,1) out of order.
One pair is mis-ordered, so the perm is odd.
A reorientation is even if it consists of an even perm and an even sig, or an odd perm and an odd sig. Otherwise the reorientation is odd and is not a physically possible reorientation of the scanner.
As a result we half the space of reorientation from the incorrect 48 which includes reflections, down to 24 which consist of pure rotations.
Yes, it would probably have been easier just to use rotation matrices.
Python Code
from itertools import permutations
import sys
def initialise():
#read the input file and set up
#scanners is a set of sets of beacon coordinates
#perms is the set of permutations of the indices (0,1,2)
with open(sys.argv[1]) as file:
data = file.readlines()
scanners = []
scanner = []
for line in data:
if ',' in line:
beacon = tuple([int(x) for x in line.strip().split(',')])
scanner.append(beacon)
elif line == '\n':
scanners.append(scanner)
scanner = []
scanners.append(scanner)
scanners = [set(scanner) for scanner in scanners]
perms = set(permutations((0,1,2)))
return scanners, perms
def parity(perms):
#returns a dictionary from permutations of (0,1,2) to the set of signatures (axis inversion) such that the total operation is parity preserving
#for example, since the permutation (1,0,2) is odd, we must choose the odd signatures (-1,1,1), (1,-1,1),(1,1,-1) and (-1,-1,-1)}
# so correct_sigs[(1,0,2)] == {(-1,1,1), (1,-1,1),(1,1,-1),(-1,-1,-1)}
correct_sigs = {}
for perm in perms:
parity = sum(1 for (x,px) in enumerate(perm) for (y,py) in enumerate(perm) if x<y and px>py)%2 #calculate parity of the permutation
if parity == 0:
correct_sigs[perm] = {(1,1,1), (-1,-1,1), (-1,1,-1), (1,-1,-1)}
if parity == 1:
correct_sigs[perm] = {(-1,1,1), (1,-1,1),(1,1,-1),(-1,-1,-1)}
return correct_sigs
scanners, perms = initialise()
correct_sigs = parity(perms)
def reorient(scanner,perm,sig):
#reorients a scanner using a particular permutation and signature
#returns the reoriented scanner (a new set of beacon coordinates)
newscanner = set()
for beacon in scanner:
newbeacon = (beacon[perm[0]]*sig[0], beacon[perm[1]]*sig[1], beacon[perm[2]]*sig[2])
newscanner.add(newbeacon)
return newscanner
def translate(scanner,offset):
#translates a scanner by a particular offset, where the offset is a tuple (dx,dy,dz) representing the translation vector
#returns the reoriented scanner (a new set of beacon coordinates)
newscanner = set()
dx,dy,dz = offset
for beacon in scanner:
x,y,z = beacon
newbeacon = (x+dx,y+dy,z+dz)
newscanner.add(newbeacon)
return newscanner
def match12(scannerA, scannerB):
#Returns True if scannerA and scannerB have 12 or more beacon coordinates in common
#otherwise returns False
common_points = scannerA.intersection(scannerB)
if len(common_points) >= 12:
return True
return False
def compare(scannerA,scannerB):
#brute force to determine if two scanners match
#check every parity preserving orientation of scanner B (permutation + signature)
#and every translation (offset) of scanner B that brings a beacon from scanner B into alignment with a beacon from scanner A
#if a match is found, return the offset, permutation and signature that matches the two scanners
#return None if no match is found
for perm in perms:
for sig in correct_sigs[perm]:
rotB = reorient(scannerB,perm,sig)
for beaconA in scannerA:
for beaconB in rotB:
xa,ya,za = beaconA
xb,yb,zb = beaconB
offset = (xa-xb,ya-yb,za-zb)
transB = translate(rotB,offset)
if match12(scannerA,transB):
return offset, perm, sig
offset = (xb-xa,yb-ya,zb-za)
transB = translate(rotB,offset)
if match12(scannerA,transB):
return offset, perm, sig
def part_two(scanners):
#the "base scanner" is a set of coordinates of beacons from the point of view of scanner 0
#when a new scanner is correctly aligned and translated, its beacons are added to the "base scanner" set
base_scanner = scanners[0]
#a list of scanners which have been incorporated into the "base scanner"
visited = [0]
#list of the offsets (translation vectors) of the other scanners from scanner 0's position
offsets = []
while len(visited) < len(scanners):
for i,scanner in enumerate(scanners):
if i in visited:
continue
result = compare(base_scanner, scanner)
if result:
offset, perm, sig = result
offsets.append(offset)
#reorient and translate the scanner into scanner 0's coordinate system
new_scanner = reorient(scanner,perm,sig)
new_scanner = translate(new_scanner,offset)
visited.append(i)
base_scanner = base_scanner | new_scanner #incorporate the scanner's beacons into the base scanner
#calculate the manhattan distance between every pair of scanners
#return the maximum manhattan distance (the puzzle solution)
manhattans = []
for off1 in offsets:
for off2 in offsets:
x1,y1,z1 = off1
x2,y2,z2 = off2
manhattans.append(abs(x2-x1) + abs(y2-y1) + abs(z2-z1))
return max(manhattans)
print(part_two(scanners))
Day 20 - Trench Map
Thoughts
A breath of fresh air after a challenging Day 19, this puzzle asks us to apply an “image enhancement” algorithm to a infinite grid of pixels. Each pixel is either light ( # ) or dark ( . ). Initially, there’s an input image made up of light and dark pixels, and all the other pixels on the infinite grid are dark.
The algorithm is a kind of cellular automaton process, not a million miles away from Conway’s Game of Life which was such a popular theme in Advent of Code 2020.
For each pixel in the image, consider the 3x3 grid of pixels with the target pixel at the centre. Starting from the top-left and reading right across each row, convert the 3x3 grid into a 9-digit binary number by treating light pixels as 1s and dark pixels as 0s. The resulting number gives an index in a 512-bit “algorithm string”, the character at that index will either be # or . , indicating the new state of the original target pixel.
This is repeated for every pixel in the original image to produce a new image.
The fact that the image lives on an infinite grid turns out to be relevant, which is the real trick on an otherwise simple procedural puzzle. Consider a dark pixel far away from any light pixels. This pixel and all its neighbours are dark, so the 3x3 grid with this pixel at the centre converts to the binary number 000000000, i.e. zero. But the algorithm string starts with #, so the new state of that dark pixel will be light.
So the whole infinite grid, apart from a small portion around the original image, will be lit up after the first iteration. Dealing with this is the cause of most of the puzzling around this puzzle, until you notice that not only is the first character of the algorithm string #, but the final character is . This turns out to be true for all inputs to this puzzle, which is a great advantage!
What this means is that any light pixel surrounded by light pixels will turn dark on the next iteration. It turns out, then, that most of the infinite grid will just oscillate between being dark and light. The only interesting part is an ever-growing region of the grid, starting with just the original input image. Each iteration, the interesting region grows by one pixel in each dimension. Outside the bounds of the interesting region, the pixels flip from dark to light and back each iteration.
In my solution this is handled by a variable oob (out of bounds). Initially, oob == '0' (dark), then it flips to '1' (light) and so on. Whenever the update function tries to get the value of a pixel outside the bounds of the current image, it will get the current value of oob.
The puzzle answer is the number of light pixels in the infinite grid after 50 iterations. Since 50 is even, most of the infinite grid will be dark at this point, so there is a finite answer!
Python Code
import sys
from collections import defaultdict
with open(sys.argv[1]) as file:
data = file.readlines()
algo = data[0].strip().replace('.','0').replace('#','1') #algorithm string
image = [line.strip().replace('.','0').replace('#','1') for line in data[2:]] #image grid as list of strings
def update(point, image, algo, oob):
#calculate the new value of a pixel based on its neighbours
#and the algorithm
xmax = len(image[0])-1
ymax = len(image)-1
(x,y) = point
steps = [(-1,-1), (0,-1), (1,-1), (-1,0), (0,0),(1,0),(-1,1),(0,1),(1,1)]
idx = ''
for step in steps:
(dx,dy) = step
if 0 <= x+dx <= xmax and 0 <= y+dy <= ymax:
#if in the bounds of the grid, return the value
idx += image[y+dy][x+dx]
else:
#if out of bounds, return current value of oob
idx += oob
idx = int(idx,2)
return algo[idx]
def apply_algo(image,algo, oob):
#apply the enhancement algorithm once to the image grid
#return the new image grid
image2 = []
xmax = len(image[0])-1
ymax = len(image)-1
for y in range(-1,ymax+2):
new_row = ''
for x in range(-1,xmax+2):
new_row += update((x,y), image, algo, oob)
image2.append(new_row)
return image2
def print_image(image):
#helper function to print image
#only used for debugging
for row in image:
print(row)
def part_one(image,algo,n):
#apply the enhancement algorithm n times to the initial image grid
oob = '0'
for _ in range(n):
#apply the enhancement algorithm
image = apply_algo(image,algo,oob)
#update the value of oob
if algo[0]=='1' and algo[-1]=='0' and oob == '0':
oob = '1'
elif algo[0]=='1' and algo[-1]=='0' and oob == '1':
oob = '0'
count = 0
for row in image:
for x in row:
count += int(x)
return count, image
pix_sum, img = part_one(image,algo,50)
print(pix_sum)