Advent Of Code 2021 Days 6-10
Advent of Code 2021 Days 6-10

Welcome back to some more Advent of Code 2021!
These posts will be quite brief, just a few thoughts on each puzzle and the Python 3 code I used to solve it. All code on Github here. The code below is for Part 2 of each day, which often incorporates Part 1 in some way.
Day 6 - Lanternfish
Thoughts
Here we are dealing with exponential growth of a population of lanternfish. Each lanternfish has its own “timer”, counting down by 1 for each day that passes. The day after a lanternfish reaches 0 days on its timer, it spawns a new lanternfish with 8 days on its timer, and resets its own timer to 8 days.
Part 1 of the puzzle was to find out how many lanternfish there are after 80 days. While you’re doing part 1, you don’t know what part 2 is going to ask you. The example for part 1 shows the lanternfish represented as a list of timer values, one value for each fish.
My instinct was that the order of the lanternfish didn’t matter, so there was no need to keep track of individual lanternfish. Fortunately, part 2 only asked for the number of lanternfish after 256 days, rather than switching to a problem where the order mattered!
Basically the question was trying to trick you into representing lanternfish individually, and thus gobbling up all your computer’s memory due to the exponential rate of growth. Instead, the code below tracks the population of lanternfish with each timer value. This is done with a defaultdict from timer value to population. The defaultdict returns 0 if the key isn’t found, which saves having to initialise populations of zero in each state.
Python Code
import sys
from collections import defaultdict
with open(sys.argv[1]) as file:
data = file.read().split(',')
data = [int(x) for x in data]
counts = defaultdict(lambda: 0)
for x in data:
counts[x] += 1
def advance(state):
newstate = defaultdict(lambda: 0)
for t in range(8,-1,-1):
if t==8:
newstate[8] = state[0]
elif t==6:
newstate[6] = state[7] + state[0]
else:
newstate[t] = state[t+1]
return newstate
generations = 256
for i in range(generations):
counts = advance(counts)
print(sum(counts.values()))
Day 7 - The Treachery of Whales
Thoughts
Crab submarines can only move horizontally. Their own limitations are represented in their technology, a salutary lesson for any software developer. Or maybe I’m reading too much into it.
We have many crab submarines at different horizontal positions, and we want to find the minimum fuel cost required to bring them all into alignment. The fuel cost of moving a crab submarine is based on triangular numbers - the first step costs 1 fuel, the second step costs 2, and so on. So moving from position 13 to 17 would cost (1+2+3+4) = 10 fuel.
Moving n steps therefore costs 0.5(n)(n+1) units of fuel, thanks to the well known formula for triangular numbers due to the great Carl Friedrich Gauss.
What you see below is a brute force solution to the minimisation problem. The code simply iterates through each candidate position x, and works out the total fuel cost of aligning all the crab submarines at that position.
There are of course many improvements that could be made here. The total cost function is convex, so gradient descent would do a good job of finding the minimum.
Furthermore, it can be shown that the optimum position lies within 0.5 of the mean of the initial positions. If you’re willing to follow a proof of that or take it on faith, you can solve this problem by checking only two values. Try cost(floor(mean)) and cost(ceil(mean)), and take the lowest, which will be the overall minimum fuel cost.
(I’m actually a bit suspicious of the continuous calculus that goes into some “proofs” of the result that the optimum position lies within 0.5 of the mean, but the result appears to be true and can be shown without calculus, albeit it gets a bit messy).
Python Code
import sys
with open(sys.argv[1]) as file:
data = file.read().split(',')
data = [int(val) for val in data]
def sum_fuel_costs(positions, x):
sum = 0
for position in positions:
d = abs(position-x)
sum += 0.5*d*(d+1)
return int(sum)
min_cost = sum_fuel_costs(data,0)
#brute force solution
for x in range(min(data),max(data)):
cost = sum_fuel_costs(data,x)
if cost < min_cost:
min_cost = cost
print(min_cost)
Day 8 - Seven Segment Search
Thoughts
This is a fun one!
We have a bunch of badly mis-wired seven-segment displays to deal with.
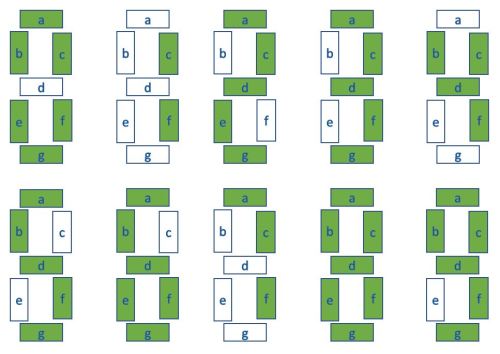
The displays represent the digits 0-9 as shown in the diagram below, with segments labelled a to g.
For each 4 digit display in the input, we get a list of what all ten possible digits look like, plus the four digits the display is actually trying to show. Each display is miswired in a different way, so the 10 possible digits will not look like the above diagram! Each display always lights up the correct number of segments, but the segments have been mixed up in a consistent way. For example, a certain display might light up segment f every time it is supposed to light up segment b.
While this mapping will be consistent within a given display, each display is mis-wired differently. Each line of the input is effectively its own mini-puzzle that needs to be solved, independent of the other lines.
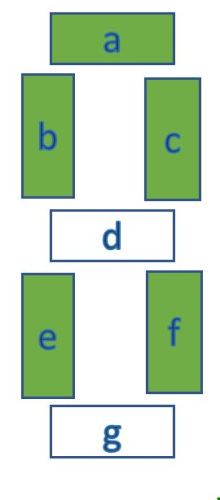
The scrambled seven-segment displays are represented by strings, for example febca, showing which segments are lit. febca would represent the following display:
Let’s look at an example line of our input, representing various configurations of a single mis-wired display:
febca cfagb ecbafd efdcbg cbegdfa fg bgafec gfae acgdb gfc | cgf facdeb ecgfdb afcbge
On the left of the | character we have all the digits 0-9, as they are shown on this mis-wired display. These could be in any order.
On the right of the | character we have the 4 digit output that we need to decode.
Consider the display gfc. This can only represent the digit 7, because 7 is the only digit where exactly 3 segments are lit. This means that the first digit of the output, cgf, must be 7. Notice that the order of the characters doesn’t matter - if the same segments are lit, the same digit is being displayed. This is one of the reasons my solution makes heavy use of sets - sets do not have any internal ordering. {g,f,c} and {c,g,f} are identical sets.
In fact I use frozensets because they are immutable and hashable, and thus can be used as keys for a defaultdict.
We can decode the entire output just by thinking about sets of segments which are lit. At no point do we actually need to figure out exactly how the segments are mis-wired.
Firstly let’s organise the digits by the number of segments lit, with a quick glance at the diagram above.
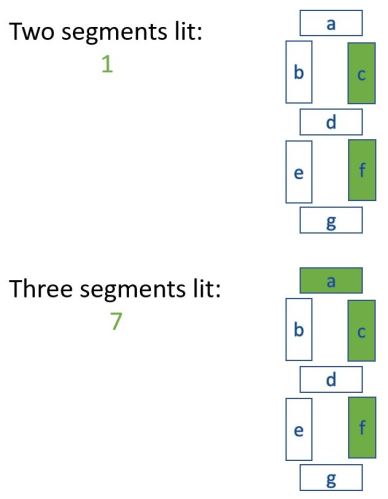
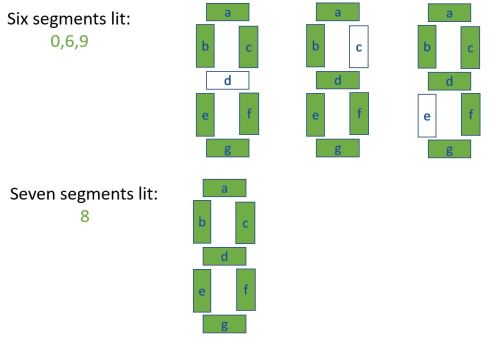
The digits 1, 4, 7, and 8 can be identified immediately by the number of segments lit.
There are a number of ways to identify the remaining digits, I used the following logic just because it was the first system that occurred to me which would work.
Compare the unidentified sets of segments with the ones that have already been identified as 7 and 4.
First consider 2, 3 and 5. Each of these has exactly five segments lit.
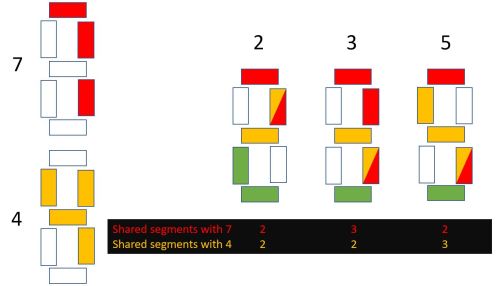
- Only 3 has exactly three segments in common with 7
- Only 5 has exactly three segments in common with 4
- The other five-segment digit must represent 2
Now repeat the process with 0, 6 and 9, which all have exactly six segments lit.
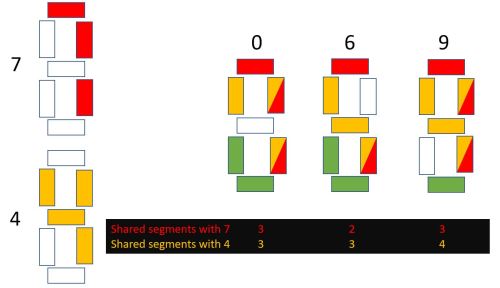
- Only 6 has exactly two segments in common with 7
- Only 9 has exactly four segments in common with 4
- The other six-segment display must represent 0
At this point we have identified how all of the digits 0-9 are represented on that particular display, and can decode the output. The final solution to the puzzle is just the sum of all the decoded outputs. Remember we need to repeat the decoding process for each row in our input, since each display is mis-wired in a different way.
Not again that this solution doesn’t actually determine how the individual segments in each display are mis-wired. Does f get lit instead of a? Does b get lit instead of c? Does g get lit correctly? Not a clue, this solution assigns sets of lit segments to digits without needing to answer any such questions.
Python Code
import sys
from collections import defaultdict
with open(sys.argv[1]) as file:
data = file.read().splitlines()
signals = []
outputs = []
for line in data:
line = line.split('|')
signal = line[0].split(' ')
signal.remove('')
output = line[1].split(' ')
output.remove('')
signals.append(signal)
outputs.append(output)
def decode(signal):
decoder = defaultdict(lambda: '.')
segs = defaultdict(lambda: [])
for x in signal:
segs[len(x)].append(frozenset(x))
if len(x) == 2:
decoder[frozenset(x)] = '1'
elif len(x) == 4:
decoder[frozenset(x)] = '4'
elif len(x) == 3:
decoder[frozenset(x)] = '7'
elif len(x) == 7:
decoder[frozenset(x)] = '8'
for y in segs[5]:
overlap_with_7 = len(y.intersection(segs[3][0]))
overlap_with_4 = len(y.intersection(segs[4][0]))
if overlap_with_7 == 3:
decoder[y] = '3'
elif overlap_with_4 == 3:
decoder[y] = '5'
else:
decoder[y] = '2'
for z in segs[6]:
overlap_with_7 = len(z.intersection(segs[3][0]))
overlap_with_4 = len(z.intersection(segs[4][0]))
if overlap_with_7 == 2:
decoder[z] = '6'
elif overlap_with_4 == 4:
decoder[z] = '9'
else:
decoder[z] = '0'
return decoder
def decode_outputs(signals,outputs):
decoded_outputs=[]
for signal,output in zip(signals,outputs):
decoder = decode(signal)
decoded_output = ''
for x in output:
decoded_output += decoder[frozenset(x)]
decoded_outputs.append(int(decoded_output))
return decoded_outputs
print(sum(decode_outputs(signals,outputs)))
Day 9 - Smoke Basin
Thoughts
Here we are dealing smoke, regarded as a fluid that flows to the lowest point of the area it is in. The height map of the region is represented by a grid of integers. The integers, ranging from 0 to 9, represent the height of that particular point on the grid.
In part 1 we have to identify low points - points which have a lower height than all adjacent points.
In part 2 we are told that a basin is a set of points that would flow down to the same low point. The input is constructed such that every basin has only a single low point. All points lie in a single basin except points with height 9, which are not considered to lie in any basin.
Our goal is to find the 3 largest basins, and multiply the number of points in each basin together.
I solved this by building a recursive function which would label every point with the basin ID of the low point that it drains to. High points (where height=9) are assigned a basin ID of -1, to represent that high points are not in any basin.
To find the basin ID of each point, I use a recursive function get_basin_ID. This function assigns any high point a basin ID of -1, and returns the basin ID of a point if already known. If the basin ID of the point is not yet known, the function recurses, considering the lowest point adjacent to the original point. Eventually the function will either reach a point whose basin ID we already know, or a low point we have not yet assigned a basin ID to. In the latter case, we assign a new basin ID to the low point.
Once every point has been assigned a basin ID, we simply count the number of points with a given ID to find the basin size, find the three largest basins, and multiply their sizes together.
Alternative Solution - Flood Fill
Now it turns out the above is actually excessive work, since all we need to do is find the size of each basin. The individual heights inside the basin are actually irrelevant - a basin can be defined as any region bounded by points with height 9. As an alternative solution, I implemented a Flood Fill which starts at a low point and fills the surrounding basin with 9s, counting the points as it goes along.
Python Code (basin ID solution)
import sys
from collections import defaultdict, Counter
from functools import reduce
import operator
from random import randint
with open(sys.argv[1]) as file:
data = file.read().splitlines()
# Since all the grid heights are between 0 and 9, 100 is a suitable default value
grid = defaultdict(lambda: 100)
for j, row in enumerate(data):
for i, item in enumerate(row):
grid[(i,j)] = int(item)
rows = len(data)
cols = len(data[0])
def neighbour_coords(i,j,grid):
#returns a list of coords of points adjacent to (i,j) in the grid
coords_list = []
steps = [(1,0),(-1,0),(0,1),(0,-1)]
for step in steps:
(dx,dy) = step
if grid[(i+dx,j+dy)] != 100: #default value is 100 if (i+dx,j_dy) is not already in grid
coords_list.append((i+dx,j+dy))
return coords_list
def get_basin_ID(i,j,grid,basin_IDs):
#recursive function to calculate the basin ID of a grid position (i,j)
#high points (height=9) will be assigned basin ID = -1
#other points will be assigned the same ID as the low point of the basin they are in
if basin_IDs[(i,j)] >= -1:
#if the basin ID of the point (i,j) is already known, return the known value
return basin_IDs[(i,j)]
elif grid[(i,j)] == 9:
#assign high points a basin ID of -1
basin_IDs[(i,j)] = -1
return -1
else:
#find the value and coords of the lowest point neighbouring (i,j)
neigh_coords = neighbour_coords(i,j,grid)
neigh_vals = {grid[(x,y)]:(x,y) for (x,y) in neigh_coords}
min_value = min(neigh_vals.keys())
min_coords = neigh_vals[min_value]
if grid[(i,j)] < min_value:
#if (i,j) is a new low point, we need to assign it a new basin ID
new_basin_ID = max(basin_IDs.values()) + 1
basin_IDs[(i,j)] = new_basin_ID
#print('new basin ID ', new_basin_ID)
return new_basin_ID
else:
#if (i,j) is not known, and is not a new low point
#recursively call the function for the coords of the lowest neighbouring point
#this recursion will eventually reach a previously known value or a new low point
#in either case the basin ID of the original point will match this value
return get_basin_ID(min_coords[0], min_coords[1], grid, basin_IDs)
def find_basins(grid):
#populates a dictionary where the keys are the coordinates on the grid and the values are the basin IDs
#high points (height=9) will be assigned basin ID = -1
#other points will be assigned the same ID as the low point of the basin they are in
basin_IDs = defaultdict(lambda: -2) #-2 is the ID of any grid position that has not been assigned a basin yet
for j in range(rows):
for i in range(cols):
#print('grid coords ', (i,j))
basin_IDs[(i,j)] = get_basin_ID(i,j,grid,basin_IDs)
return basin_IDs
def three_largest_basins(basin_IDs):
#The high points (height=9) were assigned basin ID = -1
#high points are not in any basin so should not be counted
counts = Counter([x for x in basin_IDs.values() if x >=0])
counts_list = sorted(list(counts.values()), reverse=True)
return reduce(operator.mul,counts_list[:3],1)
basin_IDs = find_basins(grid)
total = three_largest_basins(basin_IDs)
print(total)
Python Code (flood fill solution)
import sys
from collections import defaultdict, Counter
from functools import reduce
import operator
with open(sys.argv[1]) as file:
data = file.read().splitlines()
# Since all the grid heights are between 0 and 9, 10 is a suitable default value
# When the grid dictionary is asked to look up coords beyond the grid, it will return 10
# this ensures that coords beyond the grid will result in a value lower than coords within the grid
grid = defaultdict(lambda: 10)
for j, row in enumerate(data):
for i, item in enumerate(row):
grid[(i,j)] = int(item)
def neighbours(i,j,grid):
neigh_list = []
steps = [(1,0),(-1,0),(0,1),(0,-1)]
for step in steps:
(dx,dy) = step
neigh_list.append(grid[(i+dx,j+dy)])
return neigh_list
def neighbour_coords(i,j,grid):
#returns a list of coords of points adjacent to (i,j) in the grid
coords_list = []
steps = [(1,0),(-1,0),(0,1),(0,-1)]
for step in steps:
(dx,dy) = step
if grid[(i+dx,j+dy)] != 10: #default value is 10 if (i+dx,j_dy) is not already in grid
coords_list.append((i+dx,j+dy))
return coords_list
def find_low_points(grid):
low_points = []
for j, row in enumerate(data):
for i, _ in enumerate(row):
if grid[(i,j)] < min(neighbours(i,j,grid)):
low_points.append((i,j))
return low_points
def flood_fill_and_count(point,grid):
#starting with a point (x,y) that is in a basin (e.g. the low point)
#count all the points in that basin
#note that every basin is entirely surrounded by points with height 9
count = 0
if grid[point] == 9:
#stop if you've reached the edge of the basin
#or a point that's already been counted (see below)
return count
else:
count += 1 #count this point
grid[point] = 9 #flood fill with 9s, prevents counting this point again
#recursively count the neighbouring points
for nb in neighbour_coords(point[0], point[1], grid):
count += flood_fill_and_count(nb,grid)
return count
def find_basin_sizes(low_points, grid):
basin_sizes = []
for lp in low_points:
basin_sizes.append(flood_fill_and_count(lp,grid))
return basin_sizes
def solve_puzzle(grid):
lps = find_low_points(grid)
basin_sizes = find_basin_sizes(lps, grid)
return reduce(operator.mul,sorted(basin_sizes, reverse=True)[:3],1)
print(solve_puzzle(grid))
Day 10 - Syntax Scoring
Thoughts
OK, a parsing puzzle. Not my strongest area, and interesting to learn about!
In part 2 our goal is simple, correct the unbalanced brackets. There are four kinds of bracket: (), [], {} and <>. Of course these brackets can be nested.
An example string in the input would be {<{}]>} . Strings like these are called corrupted, because the character ] appears without an opening [. In part 2 we need to identify corrupted strings, but we can subsequently ignore them.
Another example might be {<(([])). This string is merely incomplete, it can be corrected by appending the completion string >} at the end to close the unbalanced brackets. For incomplete strings, we calculate a score based on the on the completion string.
The score is determined by considering the completion string character-by-character. Start with a total score of 0. Then, for each character, multiply the total score by 5 and then increase the total score by the point value given for the character below:
{
")": "1 point",
"]": "2 points",
"}": "3 points",
">": "4 points"
}
To solve this problem I implemented a stack based parser function called completion_string. The stack is implemented as a list unimaginatively titled stack. The parser moves through the line, one character at a time:
- If the current character is an opening bracket character of any kind, that character gets pushed onto the top of the stack.
-
If the current character is a closing bracket character of any kind, the current character should be the matching closing bracket for whichever type of opening bracket is at the top of the stack. This is to say, a legal closing bracket character must close the most recent bracket which is currently open.
-
If this is true, pop the opening bracket from the top of the stack and move on to the next character.
-
If this is false, the current character is illegal and the line is corrupted. In this case the function
completion_stringreturnsFalse. Any further characters in the line are irrelevant.
-
If the parser reaches the end of the string, the line must be incomplete, since the puzzle states that none of the lines of the input are correct.
How do we get the completion string which we want to return? Well, our stack still contains all the opening bracket characters which have yet to be closed. All we need to do is reverse the stack, map each character onto the matching closing character, and there’s your completion string. Ready for scoring!
To get a final solution we just need to score every completion string and find the median score.
Python Code
import sys
from statistics import median
with open(sys.argv[1]) as file:
data = file.read().splitlines()
bracketmap = {')':'(', ']': '[', '}': '{','>':'<'}
invbracketmap = {value:key for key,value in bracketmap.items()}
openers = set(bracketmap.values())
def completion_string(line):
stack = []
for char in line:
if char in openers:
stack.append(char)
else:
if stack[-1] == bracketmap[char]:
stack.pop()
else:
return False
stack.reverse()
stack = ''.join([invbracketmap[x] for x in stack])
return stack
def score(string):
scoremap = {')':1, ']':2, '}':3, '>':4}
score = 0
for char in string:
score = score*5 + scoremap[char]
return score
def solve_part_two(lines):
scores = [score(completion_string(line)) for line in lines if completion_string(line)]
return(median(scores))
print(solve_part_two(data))