Doubting Tau A Question Of %Cf%80

Doubting Tau - a question of π

I’ve spent a lot of my life talking about π. Seven years as a maths educator will do that to a person.

But I have a dark secret - every time I taught a class of students about everyone’s favourite transcendental number, I felt a twinge of pain. Because, deep down, I suspected that π wasn’t a very sensible constant to work with.

Defining π

There are various mathematical formulae that evaluate to π. That said, most people would agree that a good definition of π would be the ratio of the circumference of a circle to its diameter. We could use the formula below as a fundamental definition of π , where C is the circumference of a circle and d is the diameter.

C = π d

Already we run into a question - does this embody a relation between properties that are fundamental to a circle?

Circumference is not a particularly unique property of a circle, it’s just a special name for the property we call perimeter. Every shape has a perimeter, that’s nothing special. But it seems a reasonable property to want to calculate.

Diameter, however, is on slightly shaky ground. Every circle has a fixed diameter, it is true, but the circle isn’t the only 2D shape that has the property of having a constant width regardless of orientation. So you can define a “diameter” for many kinds of shape, such as the Reuleaux triangle.

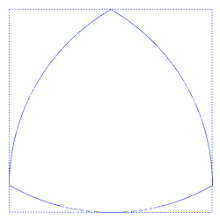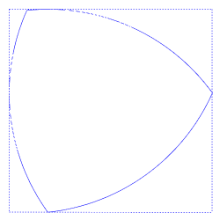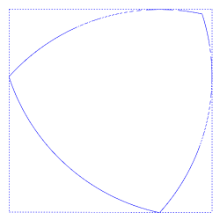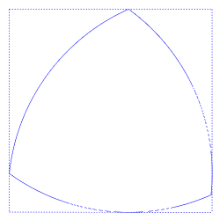
This Reuleaux triangle is not a circle, but it does have a constant width, regardless of how it rotates. This is shown by the shape always touching all 4 sides of the square.

Such shapes of constant width will crop up again later in this post.

A circle is the only shape defined by a radius. A circle is a set of points which lie an equal distance from a given point. The point is the centre, the distance is the radius.

So maybe C = 2π r , where r is the radius, makes more sense as a fundamental equation.

Enter τ

If we accept the previous argument that the relationship between C and r is the crucial relationship, why should we use π at all? The proper constant, based on that argument, would be 2π.

If history had gone differently, we might have used a constant twice as big as π. Some mathematicians have argued that this would be a better approach. They call their alternative circle constant by the name τ (Greek letter “tau”).

τ = 2π

C = τ r

Twice as Good: The Benefits of Tau

The expression 2π crops up all over the place in mathematics. It’s the value of a full turn in the radian angle measure that is fundamental to trigonometry. 360 degrees is equivalent to 2π radians. So π is half a turn, the equivalent of 180 degrees.

If we used τ instead, a full turn would be τ radians. Half a turn would be half of τ. Neat, isn’t it? The diagram below shows angles in radians in terms of τ , in all their intuitive neatness.

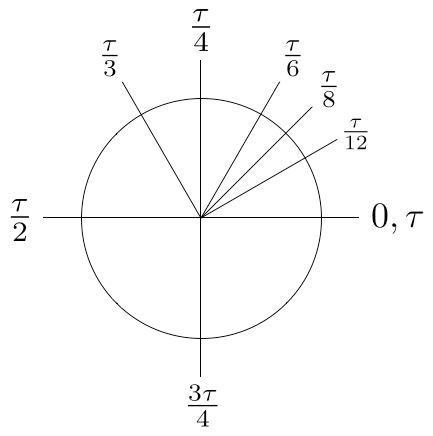
Examples of special angles in terms of τ

And various other formulae, such as the Gaussian integrals so beloved of physicists and statisticians alike, would also have an unsightly 2π replaced by a clean τ. Mathematics is absolutely full of 2π , from Fourier transforms to Cauchy’s residue theorem.

Area - An Illusory Drawback

But some of you will be wondering about area. A = π r^2^ , right? Won’t that look ugly with τ ?

A = ½ τ r^2^

Doesn’t look so hot. But even this actually has its advantages.

Because of basic rules of calculus, this kind of formula is common across applied mathematics:

Kinetic energy

KE = ½ m v^2^

where m=mass, v = speed

Potential energy stored in a spring

PE = ½ k x^2^

where k=spring constant, x=extension of the spring

Distance fallen in a constant gravitational field

s = ½ g t^2^

where g=acceleration due to gravity, t=time

Bringing the circle area into the fold makes it easier to see the deep connections between different areas of maths via calculus.

Volume - Archimedes’ Cylinder

The volume of a sphere has the charming formula, where r is the radius of the sphere:

V = (4/3) π r^3^

This isn’t a particularly pleasant-looking thing. Does τ improve matters? 2⁄3

V = 2⁄3 τ r^3^

At first glance this doesn’t look any nicer. The fraction at the front hasn’t gone away.

But there is an insight to be gleaned from this way of writing it. τ r^3^ is the volume of a cylinder with radius r and height 2r. This cylinder would completely enclose the sphere, just touching it, as shown below:

A sphere inside the smallest cylinder that could enclose it.

To verify this:

The base of the cylinder has area ½ τ r^2^ (equivalent to the familiar π r^2^ ).

Multiply the area of the base by the height ½ τ r^2^ x 2r = τ r^3^

So what this formula shows, very intuitively, is that every sphere has a volume equal to two-thirds of the volume of a cylinder that just encloses it! This amazing result was first discovered by Archimedes, and his discovery is showcased very clearly in a notation that uses τ instead of π.

Barbier’s Theorem - Reason to Doubt

So far I’ve been summarising and agreeing with the Tau Manifesto. τ makes numerous formulae look nicer, and makes the area formula (which looks worse) actually fit into its mathematical niche more obviously.

But there is a problem here, and it comes back to those shapes of constant width I was talking about earlier.

Every shape of constant width obeys Barbier’s theorem. Namely, that the perimeter of such shapes is always equal to π multiplied by the width, or diameter.

Remember that circumference is just a fancy word for “perimeter”, used for the perimeter of a circle in particular. Turns out a circle is just an example of a shape of constant diameter, and the formula for circumference is just a special case of Barbier’s theorem.

P = π d

where P is the perimeter of any shape with a constant width (or diameter) d.

This suggests that a diameter actually is a more fundamental property than a radius. Lots of shapes have a constant diameter, only one has a constant radius. We can’t use P = 2π r or P = τ r because there is no “radius” for, say, a Reuleaux polygon. There’s no constant distance from the centre to the edge of the shape.

Sure, we could arbitrarily define r as equal to half the diameter, but that’s just playing notational games.

There’s something here which suggests that a constant based on the diameter might have a broader applicability that a constant based on the radius. This is definitely a point in favour of our familiar friend π.

Confused Conclusion

Thinking about Barbier’s theorem suggests that the relationship between diameter and perimeter is more fundamental than the one between radius and perimeter. That gives primacy to π as the constant of choice. But then you have to face a world where a full turn is 2π radians and the area formula doesn’t fit as neatly with its mathematical bedfellows.

The world we’ve all lived in since childhood, but a world that could be different.

To tau or not to tau, that is the question.